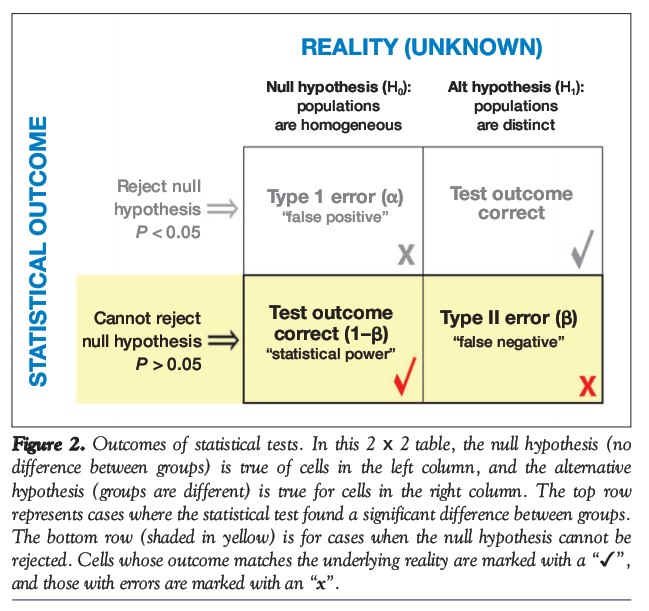
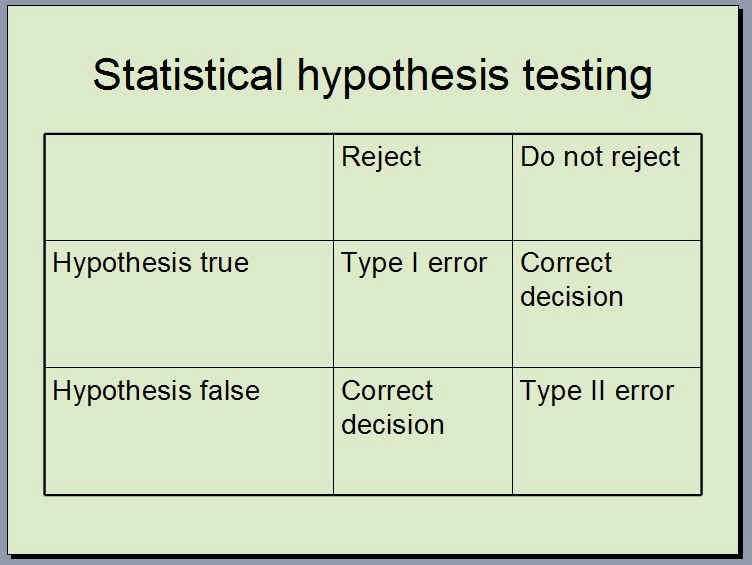
errors

Type I	Type II
false positives	false negatives
rejecting a true hypothesis of no difference or of no effect (you say there's a difference when there really isn't one)	failing to reject a false hypothesis of no difference or of no effect (you say there's no difference when there really is one)
e.g., a null hypothesis is that there is no difference in abundance of a species in habitat types A and B; the actual case is that there is indeed no difference; and the error would be in rejecting the null hypothesis, thereby concluding that there is a difference when there actually is not a difference	e.g., a null hypothesis is that there is no difference in abundance of a species in habitat types A and B; the actual case is that there IS a difference; and the error would be in failing to rejecting the null hypothesis, thereby concluding that there is no difference when there actually is a difference
e.g., if a model predicts that a species is present in a particular habitat when, in fact, it is absent	e.g., if a model predicts absence of a species in a particular habitat when, in fact, it is present
errors of commission	errors of ommission
ά = Type I error rate confidence = (1-ά)	β = Type II error rate power = (1-β)

 

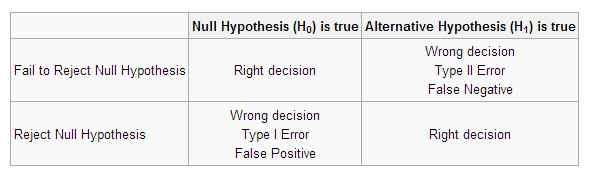
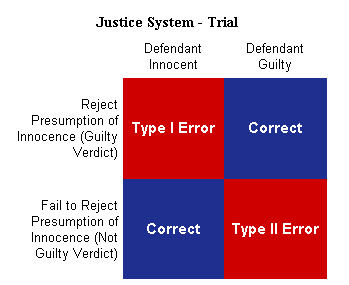
The above two figures are from
http://www.intuitor.com/statistics/T1T2Errors.html.

See also this Java applet that calculates Type I & II errors:
http://www.intuitor.com/statistics/CurveApplet.html.
  
  

On Simpson's Paradox:
http://www.intuitor.com/statistics/SimpsonsParadox.html.